
Abbiamo visto per linee generali come funziona un orologio. Proviamo ora ad entrare nei dettagli, a capire in che modo l'energia che passa dalla molla al bilanciere possa essere trasformata in un misuratore di secondi.
Iniziamo con l'analizzare il gruppo bilanciere-spirale: immaginiamo un bilanciere che possa muoversi liberamente, avendo fissata l'estremità della spirale al ponte (è sufficiente levare l'àncora) e diamo una piccola spinta al suo volantino: la prima cosa che noteremo sarà che, grazie alla spirale ed al suo espandersi e contrarsi, si muoverà avanti e indietro con ampiezze sempre minori fino a fermarsi del tutto: definiamo subito questo movimento.
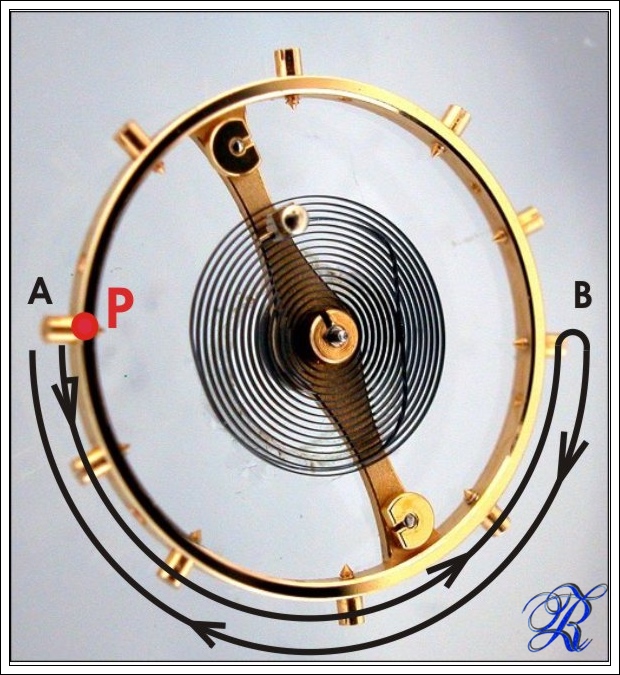
Definiamo “oscillazione” il percorso che fa un punto P nel volantino del bilanciere partendo da A per arrivare a B e tornare ad A. La metà esatta di questo viaggio, e cioè il percorso A-B (o il ritorno B-A) è detta “alternanza”.
Abbiamo così chiarito cosa significa avere un orologio che fa 18.000 alternanze/ora: vuol dire che compie per 9000 volte il percorso A-B e per altre 9000 il ritorno B-A
Se fossimo in mancanza di attriti, avremmo risolto subito il primo dei nostri problemi, perché il bilanciere continuerebbe a marciare all'infinito. Ma nella realtà queste oscillazioni diminuiranno progressivamente di ampiezza per arrestarsi poi del tutto.
Quello che ci interessa però è vedere che le oscillazioni saranno sempre della medesima durata, pur diminuendo di ampiezza: questo perchè diminuisce la distanza percorsa, ma diminuisce anche la velocità del punto P. Ci troviamo di fronte ad un fenomeno periodico ed isocrono.
Noi dobbiamo fare in modo che questo movimento resti costante nel tempo, e non si esaurisca dopo poche oscillazioni: per fare questo dobbiamo rinnovare periodicamente la spinta che abbiamo dato all'inizio.
Questo è possibile dando dei piccoli impulsi al bilanciere attraverso l'àncora, che a sua volta riceve l'impulso dalla ruota di scappamento.

L àncora agisce sul bilanciere con la sua parte terminale chiamata “forchetta” (F) che lavora sul bottone del disco (B) del bilanciere:
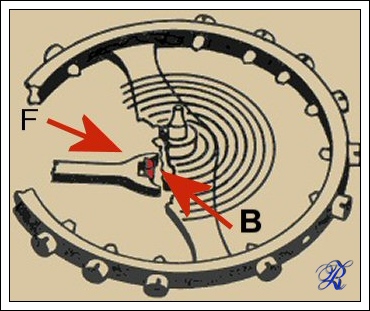
Dall'altra parte l'àncora ha due leve che, ricevendo l'impulso dalla ruota di scappamento, trasformano il moto rotatorio della ruota stessa in moto alternativo del bilanciere:
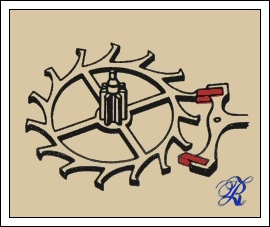
Ora però dobbiamo fare in modo che queste alternanze si possano contare e riportare in maniera leggibile: entra in gioco quindi il treno di ruote che dalla molla trasmette il moto al bilanciere.
Per rendere semplice il discorso, dobbiamo fare riferimento alla ruota centro, che possiamo individuare nel disegno, al N° 4.
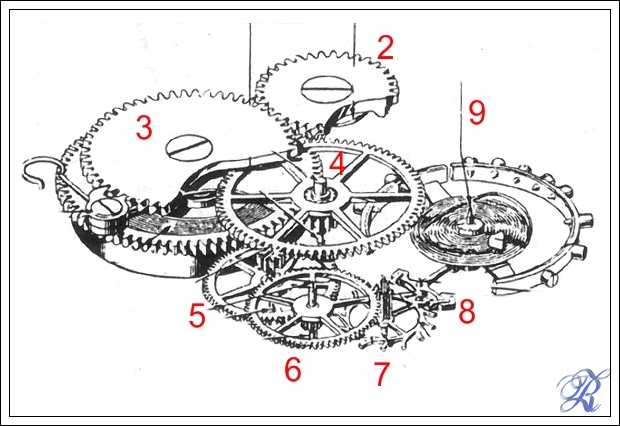
E' infatti sul perno della ruota centro che viene innestata la lancetta dei minuti e da questo prende il moto anche la lancetta delle ore.
Nel caso del nostro orologio dobbiamo fare in modo che alle 18.000 alternanze/ora del bilanciere corrisponda un giro completo della ruota centro e di conseguenza della lancetta dei minuti.
Vediamo prima come è fatta una ruota di un orologio: dal disegno sopra, possiamo vedere che di solito è composta da una ruota dentata vera e propria, generalmente in ottone, fissata ad un asse in acciaio chiamato pignone, anch'esso dentato: i denti del pignone tradizionalmente vengono chiamati ali.
Come si può notare nel disegno, ogni ruota ingrana col pignone della ruota successiva, fino ad arrivare alla ruota di scappamento che lavora con l'àncora.
Per calcolare il numero di denti delle varie ruote si usa il rapporto di trasmissione: senza entrare nei dettagli, bisogna calcolare il numero di giri che deve fare ciascuna ruota per farne compiere un numero proporzionalmente adeguato alla successiva, fino ad arrivare al famoso giro della ruota centro in un ora.
Facciamo un esempio: se la ruota centro ha 80 denti, la ruota intermedia ha 75 denti ed il suo pignone 10 ali, la ruota secondi 80 denti ed il suo pignone 10 ali, la ruota di scappamento ha 15 denti ed il suo pignone 8 ali, il rapporto di trasmissione sarà dato dal prodotto dei denti delle ruote diviso per il prodotto delle ali dei pignoni: avremo quindi:
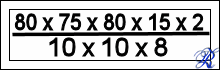
che darà 18.000 come risultato.
(il numero di denti della ruota di scappamento viene moltiplicato per 2 perché ogni dente agisce su entrambe le leve dell'àncora)
Non entriamo oltre nei dettagli, ci sono moltissime varianti che interessano la costruzione, il dimensionamento, la forma dei denti, il numero delle ruote, nel treno degli ingranaggi, ma questa è materia di studi e calcoli molto approfonditi e che non ci interessano.
Arriviamo ora alla fonte di tutta l'energia che il bilanciere ed il treno degli ingranaggi si incaricano di trasformare in un dato leggibile: la molla.
La molla è una striscia di acciaio che viene avvolta su sé stessa ed inserita in un contenitore metallico chiamato bariletto.

La molla libera deve avere approssimativamente la forma di una S, quando vediamo molle che fuori del bariletto hanno quasi tutte le spire avvolte su sè stesse, siamo di fronte ad una molla esausta e che deve essere sostituita.
La funzione del bariletto è molteplice: la molla viene inserita nel bariletto perché è più riparata dagli agenti atmosferici: la polvere che si deposita tra le spire della molla contribuisce ad aumentare di molto gli attriti e di conseguenza l'energia rilasciata dalla molla è minore e meno costante; inoltre il lubrificante messo per la molla resta più a lungo in posizione e in buone condizioni; in caso di rottura della molla, rottura che spesso avviene nella fase di massima carica della stessa, le ruote e gli ingranaggi del movimento sono al riparo della molla “impazzita”, anche se bisogna dire che questo problema si presenta comunque perché l'energia rilasciata alla molla durante la rottura si scarica sul bariletto e sulla prima ruota a contatto con esso, causandone la rottura. I danni in questo caso sono però limitati ai denti del bariletto e della ruota.
La molla è fissata alla parete del bariletto con un gancio, come si vede nel disegno. Nel corso degli anni gli attacchi delle molle hanno avuto delle evoluzioni: si è passati dal foro vero e proprio sulla molla che si fissava ad un gancio sul bariletto, agli attacchi moderni, costituiti da una piccola brida saldata alla parte terminale della molla e che va a bloccarsi in un intaglio praticato sulla parete del bariletto.
Negli orologi automatici, la brida è più lunga e non si aggancia al bariletto: serve per far slittare la molla, una volta raggiunta la massima carica, per non danneggiare il dispositivo di carica automatica.
In pratica finché la molla non è del tutto carica, la pressione delle spire esterne tiene la brida ferma contro la parete del bariletto, quando la molla si carica ulteriormente, questa pressione diminuisce, fino a far slittare la molla, scaricandola quanto basta perchè le spire esterne tornino a premere sulla brida.
Uno dei problemi che assillavano i costruttori di orologi era la poca omogeneità nell'erogazione dell'energia da parte della molla.
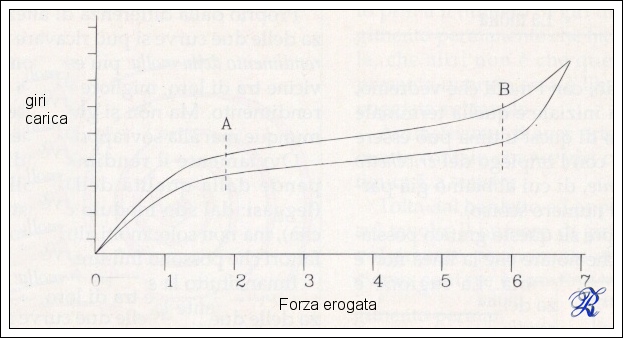
Nel grafico vediamo come la forza erogata sia molto alta quando la molla è tutta carica, mantiene un rendimento abbastanza costante durante la fase centrale del suo lavoro, per poi diminuire repentinamente l'energia erogata negli ultimi giri di carica.
Per far lavorare la molla solo nella fase centrale della sua carica, tra i punti A e B, si utilizzarono diversi dispositivi, il più famoso è la croce di Malta:
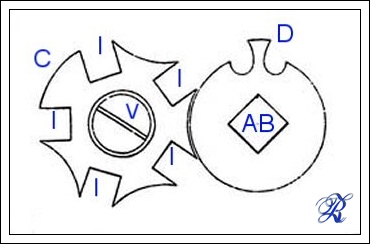
La ruota di destra, quella con un solo dito e con la sezione quadrata al centro, (AB) è quella che va fissata all'albero del bariletto, (il quadro al centro). Quando si carica l'orologio, e nel senso contrario quando si scarica, la ruota fissata all'albero del bariletto ruota anch'essa e fa spostare la ruota di sinistra,fissata al bariletto con una vite (V), ogni volta che il dito (D) trova un incavo (I).
Questo finchè non si trova la sezione concava della ruota di sx (C) che non consente più l'avanzamento della ruota trascinata dall'albero del bariletto.
Tutto questo, posizionando correttamente le due ruote, consente di non caricare e non far scaricare del tutto la molla, facendola lavorare nella sua parte centrale, ed avendo una erogazione dell'energia più stabile e costante.
Ora, con i materiali a disposizione questi dispositivi non hanno, nella pratica, ragione di essere utilizzati.
Diamo un'ultima occhiata alla formula che, in linea teorica, determina l'energia sviluppata dalla molla:
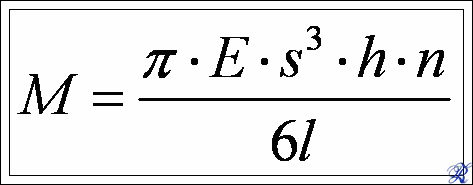
Dove M è il momento elastico (La forza della molla)
E: modulo di elasticità del materiale
s: spessore della molla
h: altezza della molla
n: numero di giri di avvolgimento
l: lunghezza della molla
La formula è teorica e si riferisce a spire che non si toccano tra loro, ma ha comunque una validità ed è messa solo per far notare quanto siano importanti certi parametri per la determinazione di una molla o di una sua sostituzione.
Se noi variamo il suo spessore infatti, tale variazione si ripercuoterà in maniera pesante perché lo spessore viene calcolato al cubo, quindi variazioni di tale parametro a prima vista non significative avranno ripercussioni abbastanza importanti sul funzionamento dell'orologio.
E' chiaro che un grafico teorico di questa formula risulterebbe improponibile da applicare ad un orologio: aumentando il numero dei giri di carica infatti la forza aumenta in proporzione e costantemente, mentre nella pratica, dalle rilevazioni fatte mediante dinamometri, il grafico è quello dato sopra.